發電壓電晶片工作效應詳解

在研究石英晶體的物理性質時發現：當沿著晶片的某些方向施加作用力使晶片發生形變后，晶片上相對的兩個表面會出現等量的正、負電荷，電荷面密度與施加的力的大小有關，該現象稱為壓電現象。具有壓電現象的介質為壓電體。

在離子性的晶體中，正負離子有規則地交錯配置，構成結晶點陣，就形成固有電矩，在晶體表面出現極化電荷，由于晶體暴露在空氣中，經過一段時間，這些電荷便被降落到晶面上的空氣中的異號離子所中和，因此，極化面電荷和電矩都不會顯現。但當晶體發生機械形變時，晶格就會發生變化。這樣，電矩產生變化，表面極化電荷數值也發生改變。于是，表面上正電荷或負電荷都有了可以測量的增量，該增量是壓電效應電量。

壓電效應分為正壓電效應和逆壓電效應。具體工作原理如圖1所示。

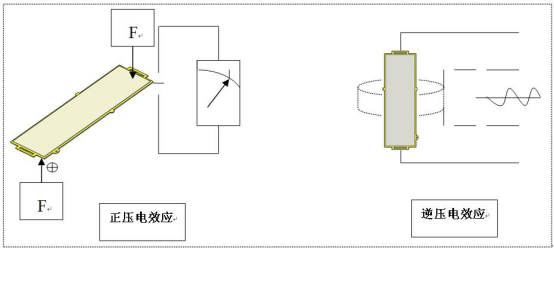
圖1 壓電效應原理

在無電場作用下，當沿著一定方向對壓電體施力而使它產生機械變形時，其內部產生極化現象，相對的兩個表面會出現異號電荷，外力與端面積大，出現的電荷就多。端面電荷的符號視外力而定。當外力去掉后，又重新恢復不帶電狀態的現象，稱為正壓電效應。當作用力方向改變時，電荷極性也隨著改變。若將兩個表面裝上電極并用導線接通，變化的自由電荷便從一個極板移至另一極板，形成電流。具有壓電效應的晶體稱為壓電晶體。

當在壓電體的極化方向施加電場時，壓電體就在一定方向上產生機械形變或機械壓力，當外電場撤去時，這些形變或壓力隨之消失的現象稱為逆壓電效應。逆壓電效應的產生，是由于壓電晶體受到電場作用時，在晶體內部產生了應力，這種應力稱為壓電應力，通過它的作用產生壓電應變。

因此，壓電效應是由于晶體在機械力的作用下發生形變而引起帶電粒子的相對位移，從而使晶體的總電矩發生變化而造成的。晶體是否呈現壓電性，由構成晶體的原子和離子排列方式決定的。具有對稱中心的晶體不可能有壓電性。凡是具有正壓電效應的晶體，也一定有逆壓電效應，具有壓電效應的材料稱為壓電材料。

1.2 壓電效應的物理機制

晶體內部正、負離子的偶極矩在外力的作用下由于晶體的形變而被破壞，導致使晶體的電中性被破壞，從而使其在一些特定的方向上的晶體表面出現剩余電電荷而產生的。

壓電陶瓷的壓電效應機理與壓電單晶大不相同，未經極化處理的壓電陶瓷材料是不會產生壓電效應的。壓電陶瓷經極化處理后，剩余極化強度會使與極化方向垂直的兩端出現束縛電荷（一端為正，另一端為負），由于這些束縛電荷的作用在陶瓷的兩個表面吸附一層來自外界的自由電荷，并使整個壓電陶瓷片呈電中性。當對其施加一個與極化方向平行或垂直的外壓力，壓電陶瓷片將會產生形變，片內束縛電荷層的間距變小，一端的束縛電荷對另一端異號的束縛電荷影響增強，而使表面的自由電荷過剩出現放電現象。當所受到的外力是拉力時，將會出現充電現象。

1.3 壓電效應產生的條件

晶體結構沒有對稱中心。

壓電體是電介質。

其結構必須有帶正負電荷的質點。即壓電體是離子晶體或由離子團組成的分子晶體。

1.4 壓電方程

在壓電彈性體中，機械效應與電效應是分不開的，它們互相牽制，緊緊耦合在一起。因此，壓電方程是壓電體的力學量（應力T，應變S）和電學量（電場強度E，電位移D）間的關系方程。表示如下：

式中是在恒定應力（或零應力）下測量出的機械自由介電常數，為電短路情況下測得的彈性常數，為壓電常數。第一個方程敘述了正壓電效應，第二個方程敘述了逆壓電效應。

1.5 壓電性能參數

壓電發電晶片利用鋯鈦酸鉛（PZT）陶瓷片的正壓電效應產生電壓和電荷，陶瓷片的壓電性能直接影響壓電發電晶片的工作性能。其壓電性能可由多個壓電參數表達，其中與發電晶片相關的參數主要為機電耦合系數，機械品質因數等�，F敘述如下：

1、機電耦合系數

機電耦合系數是綜合反映壓電材料性能的參數。它表示壓電材料的機械能與電能的耦合效應，定義為：

或

壓電元件的機械能與它的形狀和振動方式有關，不同形狀和不同振動方式所對應的機電耦合系數不同。

2、機械品質因數

壓電體作諧振動時，要克服內部的機械摩擦損耗，再有負載時要克服外部負載的損耗。機械品質因數定義為機械損耗的反比，即：

機械品質因數的存在表明任何壓電材料都不能把輸入的機械能全部用于輸出。機械品質因數越大，能量的損耗就越少。

3、頻率常數

壓電晶片元件的諧振頻率與沿振動方向的長度的乘積為一常數，即頻率常數。

表示在諧振頻率狀態下工作具有最好的輸出。

4、相對介電常數

相對介電常數反映材料的介電性質或極化性質。定義如下：

2 壓電發電鞋理論發電效率分析

壓電陶瓷片具有將機械能轉化為電能的性能，當其受外力作用時，其極化強度隨之而變, 導致表面吸附的自由電荷隨之變化。

2.1 等效模型

當一陶瓷片在壓力作用下上下表面產生電荷，其相當于一個電容，電容在其兩極產生電荷后就儲存了一定的能量。從電學角度來看，壓電片可以簡化為一個正弦電流源，與內在的電極電容 并聯，如圖2所示。假設電流源和電極電容恒定，負載可調。由戴維南等效定理，該電路中阻抗為：

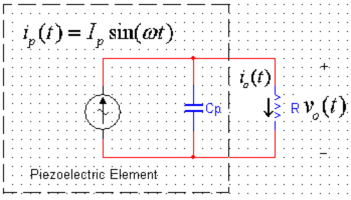
圖2 壓電片帶負載電阻的等效電路

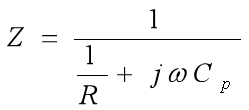即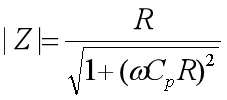     

可求出電路輸出電壓：

輸出功率:

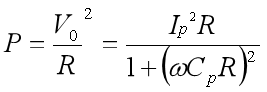
當時，即外接負載電阻和壓電片等效阻抗相等時，負載吸收的能量最大。

 發電晶片中的陶瓷片工作在厚度伸縮模式下，如圖3為壓電陶瓷片，其作用面積為A,厚度為h，沿y軸極化，沿y軸方向施加應力F。

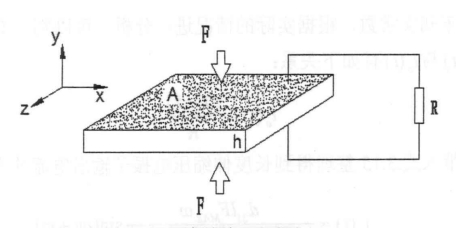
圖3 厚度伸縮壓電發電振子

在外界壓力F作用下的壓電材料產生的電荷和電壓為：

壓電片等效為一個電容，其儲能的公式是：

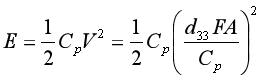
式中： 為壓電片的壓電常數；F 為作用在壓電片表面的應力； 是作用力施加的區域； h分別是壓電片的厚度；為壓電片的相對介電常數；為真空介電常數。

將上述的公式整理后可得壓電片產生的電能為：

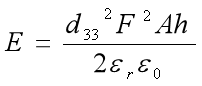
一個人走路時對發電晶片做的功可用以下公式計算：

壓電發電晶片的發電效率為;

2.2 能量傳輸和利用效率分析

當作用在壓電片上的力消失后，壓電元件產生的電荷立即消失。因此，需要外接電容對壓電元件產生的電荷進行儲存。設壓電元件極間電容為，外接電容為C，產生的電能在兩者之間再分配，根據傳輸結束后電壓相等的關系，設，其中，C 為外接電容；為壓電元件間電容；是設的量，。則電容C 上存儲的能量與產生能量的傳輸效率：

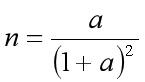
當 ，得到= 1。即時，傳輸效率最大，此時n = 25%。