動態元件組成的 動態電路及初始狀態
一、動態電路
動態電路( dynamic circuits )
動態元件具有動態性、記憶性和儲能性等特點,含有動態元件的電路叫動態電路。
含有一個獨立動態元件的電路稱為一階動態元件,電路方程是一階微分方程;含有兩個獨立動態元件的電路稱為二階動態元件,電路方程是二階微分方程。
圖 5.2-1 所示電路中, LP1 、 LP2 和 LP3 是三個白熾燈,它們分別與電阻 R 、電容 C 和電感 L 相串聯,并通過開關 S 接到直流電壓源 Us 上,開關 S 閉合之前,三個燈泡都不亮。
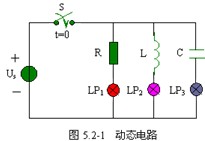
t=0 時開關 K 閉合,觀察現象
1 、與電阻 R 串聯的燈泡 LP1 立即發光,且亮度始終保持不變;
2 、與電感 L 串聯的燈泡 LP2 開始并不發光,過一會才慢慢變亮,直至亮度達到最亮,且一直保持不變;
3 、與電容 C 串聯的燈泡 LP3 立即發光,但稍后開始慢慢變暗,直至最后熄滅。
二、初始狀態
1 、換路定則
換 路( switching )
動態電路中,把某一時刻電源或無源元件的接入、斷開、某些支路的短路或開路及某些元件參數的改變稱為電路換路,而且認為換路是在即刻完成的。
電路換路,使得電路改變原來的穩定狀態,進入暫態( transient state )過程或過渡過程。當暫態過程結束后,電路又會達到新的穩定狀態,簡稱穩態( steady state )。
換路定則
電容電壓在換路瞬間不能躍變![]()
電感電流在換路瞬間不能躍變![]()
![]() 是換路前的一瞬間,
是換路前的一瞬間, ![]() 是換路后的一瞬間。
是換路后的一瞬間。![]()
注 意
電路中其它響應,如電容電流 ![]() 、電感電壓
、電感電壓 ![]() 、電阻電壓
、電阻電壓 ![]() 、電阻電流
、電阻電流 ![]() 等,都不受換路定則的約束,都有可能發生躍變。
等,都不受換路定則的約束,都有可能發生躍變。
2 、初始值的計算
初始值的計算步驟
1 、畫出 t=0 -時刻的等效電路,此時電路處于穩態。對于直流激勵,將電容視為開路,將電感視為短路,求出 ![]() 和
和 ![]() 。
。
2 、由換路定則求 t=0 +時刻的電路初始狀態,
![]()
![]()
3 、根據替代定理,用電壓為 ![]() 的電壓源和電流為
的電壓源和電流為 ![]() 的電流源替代電路中的電容和電感,作出 t=0 +時刻的等效電路,再按直流電阻電路的計算方法求出其它響應的初始值。
的電流源替代電路中的電容和電感,作出 t=0 +時刻的等效電路,再按直流電阻電路的計算方法求出其它響應的初始值。
例 5.2-1 圖 5.2-2 ( a )所示電路中,已知 ![]() 時開關 S 處于斷開狀態,且電路已處于穩態。 t=0 時刻開關 S 閉合,求 t=0 +時刻的
時開關 S 處于斷開狀態,且電路已處于穩態。 t=0 時刻開關 S 閉合,求 t=0 +時刻的 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 。
。
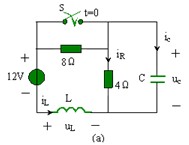
解: 1. ![]() 時電路已處于穩態,由于 12V 直流電壓源激勵,根據電容、電感的性質,可將電容視為開路,將電感視為短路,且開關 S 斷開,作出 t=0 -時刻的等效電路,如圖 5.2-2 ( b )所示。由圖 5.2-2 ( b )可知,
時電路已處于穩態,由于 12V 直流電壓源激勵,根據電容、電感的性質,可將電容視為開路,將電感視為短路,且開關 S 斷開,作出 t=0 -時刻的等效電路,如圖 5.2-2 ( b )所示。由圖 5.2-2 ( b )可知,
![]()
![]()
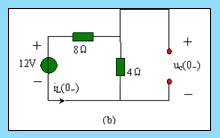
2 .由換路定則得,
![]()
3 . t=0 +時刻,由替代定理,用 4V 電壓源替代電容 C ,用 1A 的電流源替代電感 L ,且此時開關 S 閉合,得 t=0 +時刻的等效電路,如圖 5.2-2 ( c )所示。

由圖 5.2-2 ( c )得![]()
又![]()
則![]()
所以,各初始值為![]()


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底