1. 計數體制
(1)十進制數
有0,1,2,…,9等十個數碼元素,任何一個大小的數字都由這十個元素組成。例如(475.8)10或(475.8)D,這個十進制數可以寫成![]() 。它表明:進制數為10(即r=10),高低位之間關系為逢十進一,高位至低位的權值為:
。它表明:進制數為10(即r=10),高低位之間關系為逢十進一,高位至低位的權值為:![]() 。因此有通式:
。因此有通式:![]() 。式中n是該數整數部分的位數,m是小數部分的位數, Ki是i位的數碼,r是表示任意進制時的基數,如二進制數、八進制數和十六進制數等。
。式中n是該數整數部分的位數,m是小數部分的位數, Ki是i位的數碼,r是表示任意進制時的基數,如二進制數、八進制數和十六進制數等。
(2)二進制數
有0,1二個數碼元素,基數r=2,逢二進一,如:(110101.101)2或(110101.101)B,寫成通式展開后為:![]() 。高位至低位的權值為:
。高位至低位的權值為:![]() 。
。
(3)八進制數
有0,1,…,6,7等八個數碼元素,基數r=8,逢八進一,如:(356.71)8或(356.71)O,寫成通式展開后為:![]() 。 高位至低的權值為:
。 高位至低的權值為:![]() 。
。
(4)十六進制數
有0,1,2,…,9,A,B,C,D,E,F等十六個數碼元素,基數r=16,逢十六進一,如:(5A8D.C6) 16或(5A8D.C6) H,寫成通式展開后為:![]() 。
。
高位至低位的權值為:![]() 。
。
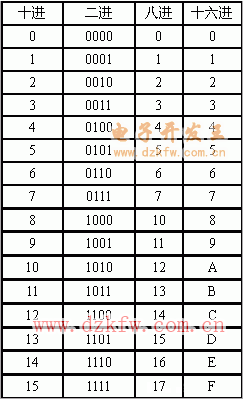
十進、二進、八進和十六進制數間關系表:
2 . 各種進制數之間的相互轉換
數字電路運行在二值的二進制數字信號下,但為書寫方便,常用八進和十六進制數表示,而日常又習慣于十進制數,所以要進行數制間的轉換。
(1)十進制數整數部分—二、八、十六進制
具體方法:將待轉換的十進制數整數除以進制數(二、八、十六)取余數,不斷地進行,直至商為零。第一次的余數為轉換后進制數的最低位(LSB:Least Siginificant Bit),最后的余數為轉換后進制數的最高位(MSB:Most Siginificant Bit)。
十進制轉換成二進制為例: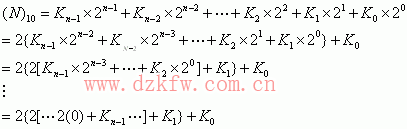
組成轉換后的二進制數為:![]() 。
。
(2)十進制數小數部分的轉換
方法:待轉換的十進制小數乘進制數(二、八、十六)取整,不斷地進行,直至積的小數為零為止。必須注意:若積的小數達不到零時,根據轉換的精度來取位數。另外,第一次的整數為轉換后進制數的最高位(MSB),即:![]() 。
。
(3)二、八、十六進制數之間的相互轉換
方法:以二進制數為橋梁進行即可。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底