【題目1】:模擬信號和數字信號有何區別?各有什么特點?
【相關知識】:模擬信號、數字信號,及其處理方法。
【解題方法】:理解題。
【解答過程】:通常講的模擬信號是指該信號的大小隨時間連讀變化的電信號,不會有突變。如正弦交流電信號,可以用下式表示。它的特點是連讀,并能用相位、幅值和時間來描述,有瞬時值,幅值等參數。

而數字信號在時間上是離散的,幅值上只區別兩個截然不同的值或狀態,而并不要求對具體的大小進行量化。兩個不同的值或狀態可以用二進制數“1”和“0”來表示。兩個不同的數值或狀態在電路上實現起來非常方便,如開關的閉合或斷開,晶體管的飽和導通或截止等等。
【題目2】:代數法化簡和卡諾圖法化簡有何聯系?
【相關知識】:邏輯函數化簡的兩種基本方法,1~5變量卡諾圖的畫法等。
【解題方法】:卡諾圖化簡其實質是合并最小項,只不過將最小項按一定規律進行排序,并在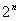 個最小項中,提取公共變量后消去其它變量,以達到簡化的目的。
個最小項中,提取公共變量后消去其它變量,以達到簡化的目的。
【解答過程】:代數法化簡邏輯函數式,是運用邏輯代數的定律、定理、規則對邏輯式進行變換,以消除多余的與項和變量。代數法化簡沒有普遍適用規律,有時需要一定的經驗和熟練的技巧。
卡諾圖法化簡的實質是合并最小項,以消除多余的變量。因為卡諾圖中的一個小方格就是一個最小項,但是小方格與小方格之間的關系必須是相鄰的關系,即卡諾圖中的上下、左右,前后小方格的最小項必須保持只有一個變量不同,其余的變量都相同,才能實現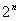 (n=1,2,3,…,整正數)個相鄰方格的最小項合并。其合并結果是消除n個變量。可見合并的最小項范圍越大,可以消除的變量就越多。這樣做非常直觀、便捷。
(n=1,2,3,…,整正數)個相鄰方格的最小項合并。其合并結果是消除n個變量。可見合并的最小項范圍越大,可以消除的變量就越多。這樣做非常直觀、便捷。
如果在已知與或表達式的情況下,將該式轉換成最小項之和式后,再象卡諾圖那樣找出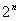 個相鄰最小項進行合并,就很困難了。可見代數法化簡和卡諾圖法化簡具有相同的內在關系,只是處理方法不一樣而已。
個相鄰最小項進行合并,就很困難了。可見代數法化簡和卡諾圖法化簡具有相同的內在關系,只是處理方法不一樣而已。
【題目3】:為什么兩個二進制數之間的減法運算可以用它們的補碼相加來實現?
【相關知識】:二進制數,二進制數的加法運算,正負二進制數的表示,二進制數的原碼、反碼和補碼表示等。
【解題方法】:可以從日常生活中的時鐘校時方法加以理解。聯系時鐘校時的兩種方法,順時針校時和反時針校時,就可以想到減法可以用補碼相加代替了。
【解答過程】:我們已經知道,在數字電路中是用邏輯電路輸出的高、低電平表示二進制數的1和0的。那么數的正、負又如何表示呢?通常采用的方法是在二進制數的前面增加一位符號位。符號位為0表示這個數是正數,符號位為1表示這個數是負數。這種形式的數稱為原碼。
在作減法運算時,如果兩個數是用原碼表示的,則首先需要比較兩數絕對值的大小,然后以絕對值大的一個作為被減數、絕對值小的一個作為減數,求出差值,并以絕對值大的一個數的符號作為差值的符號。不難看出,這個操作過程比較麻煩,而且需要使用數值比較電路和減法運算電路。如果能用兩數的補碼相加代替上述的減法運算,那么計算過程中就無需使用數值比較電路和減法運算電路了,從而使運算器的電路結構大為簡化。
為了說明補碼運算的原理,我們先來討論一個生活中常見的事例。例如你在5點鐘的時候發現自己的手表停在10點上了,因而必須把表針撥回到5點。由圖E4b20334001-01Z上可以看出,這時有兩種撥法:第一種撥法是往后撥5格,(因10-5=5),可撥回到5點;另一種撥法是往前撥7格,(因10+7=17)。由于表盤的最大數是12,超過12以后的“進位”將自動消失,于是就只剩下減去12以后的余數了,即17-12=5,由此也可把表針撥回到5點。這個例子說明,10-5的減法運算可以用10+7的加法運算代替。因為5和7相加正好等于產生進位的模數12,所以我們稱7為-5對模12的補數,也叫做補碼。

從這個例子中可以得出一個結論,就是在舍棄進位的條件下,減去某個數可以用加上它的補碼來代替。這個結論同樣適用于二進制數的運算。
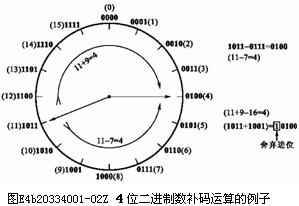
圖E4b20334001-02Z中給出了4位二進制數補碼運算的一個例子。由圖可見,1011-0111=0100的減法運算,在舍棄進位的條件下,可以用1011+1001=0100的加法運算代替。因為4位二進制數的進位基數是16(10000),所以1001(9)恰好是0111(7)對模16的補碼。
為了避免作減法運算,在求負數的補碼時可以先求出二進制數原碼的反碼(將數字代碼中每一位的取值求反,即0改為1,1改為0,符號位保持不變),然后在最低位加1而得到補碼。例如有一個4位二進制的負數,它的原碼為10101(最左邊一位是符號位),則它的反碼為11010。在反碼的最低位加1后得到補碼為11011。將這個補碼和它的原碼相加(不包括符號位),得到的正好是10000(16),也就是4位二進制數的進位基數,因此11011是10101的補碼。
至此我們可以歸納出以下幾點簡單的結論:
1.二進制數原碼的定義
二進制數的原碼是在它的數值前面設置一位符號位而得到的。正數的符號位是0,負數的符號位是1。
2. 二進制數補碼的定義
正數的補碼與原碼相同。
負數的補碼可以通過將每一位數值求反,然后在最低位加1而得到(符號位保持不變)。
3.兩個二進制數的加、減運算都可以用它們的補碼相加來實現,得到的運算結果也是補碼形式。
4. 進一步的分析表明,在將兩個數的補碼相加時,如果將兩個補碼的符號位和數值部分產生的進位相加,則得到的和就是兩個二進制數相加后代數和的符號。
例如要計算0101-1001,則可以先求出0101和-1001的補碼00101和10111(最高位為符號位),再將兩個補碼相加而得到:

如果需要求出負數補碼對應的原碼,只要對這個補碼再求一次補碼就可以得到了。
【題目4】:什么是約束項、任意項和無關項?為什么在具有約束條件的邏輯函數化簡時,應該盡量使用約束條件。用代數法化簡一個邏輯函數時,如何利用約束項使函數化成最簡?
【相關知識】:邏輯運算,邏輯函數,最小項和最大項的概念,邏輯運算中的常用公式,運算規則。
【解題方法】:通過實例,說明什么是約束項、任意茂和無關項,以及它們的異同點。
【解答過程】:我們在分析一個邏輯函數時經常會遇到這樣一類情況,就是輸入邏輯變量的某些取值始終不會出現。因此,在這些取值下等于1的那些最小項,也將始終為0。這些取值始終為0的最小項,就叫做該函數的約束項。
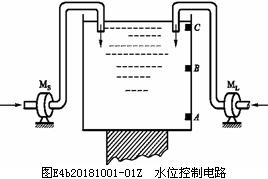
例如要求設計一個邏輯電路,用水箱中水位高度的檢測信號A、B、C控制兩個水泵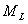 和
和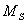 的啟、停工作狀態見圖E4b20181001-01Z。如果用
的啟、停工作狀態見圖E4b20181001-01Z。如果用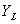 和
和 分別表示兩個水泵的工作狀態,則
分別表示兩個水泵的工作狀態,則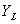 和
和 為A、B、C三個變量的邏輯函數。假定水位高于A、B、C中的任何一個檢測點時給出的檢測信號為1,水位低于任何一個檢測點時給出的檢測信號為0,則水箱工作過程中ABC的取值只可能出現100、110、111和000這四種狀態,而不可能出現001、011、101和010這四種狀態,因為水位永遠不會高于B或C而同時又低于A。因此,與ABC的取值001、011、101和010對應的四個最小項
為A、B、C三個變量的邏輯函數。假定水位高于A、B、C中的任何一個檢測點時給出的檢測信號為1,水位低于任何一個檢測點時給出的檢測信號為0,則水箱工作過程中ABC的取值只可能出現100、110、111和000這四種狀態,而不可能出現001、011、101和010這四種狀態,因為水位永遠不會高于B或C而同時又低于A。因此,與ABC的取值001、011、101和010對應的四個最小項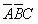 、
、 、
、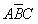 和
和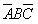 將永遠是0,這四個最小項就是
將永遠是0,這四個最小項就是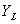 和
和 的約束項。
的約束項。
既然在工作過程中約束項的值永遠是0,那么我們就可以在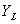 和
和 的邏輯函數式中加上這些約束項,或不加上這些約束項,而不會影響
的邏輯函數式中加上這些約束項,或不加上這些約束項,而不會影響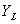 和
和 的取值。也就是說
的取值。也就是說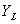 和
和 的取值與是否加上了約束項沒有關系,因此約束項又是邏輯函數式中的無關項。
的取值與是否加上了約束項沒有關系,因此約束項又是邏輯函數式中的無關項。
在分析和設計邏輯電路時,還可能遇到另外一種情況,就是在輸入變量的某些取值下,邏輯函數值等于1還是等于0都可以,對電路的邏輯功能沒有影響。在這些變量取值下等于1的那些最小項,就叫做這個邏輯函數的任意項。
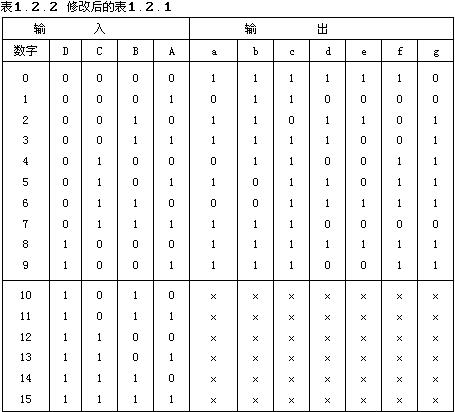
例如要設計一個拒絕偽碼的七段顯示譯碼器,其真值表如表1.2.1。所謂拒絕偽碼,系指在輸入為1010~1111時輸出無任何字形顯示,即a~g輸出全都等于0。
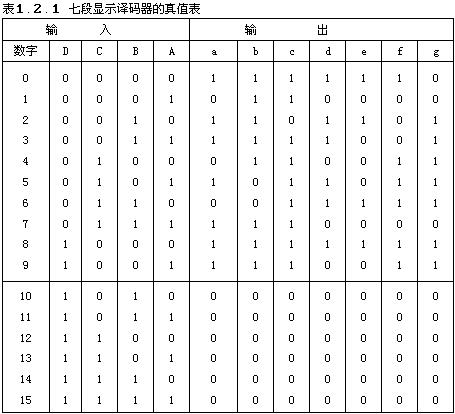
由表1.2.1可以看出,這個譯碼器是一個有4個輸入變量和7個輸出函數的組合邏輯電路。如果我們采用圖E4b20181001-01Z的電路結構,在a~g的輸出端增加一級緩沖器,同時還在緩沖器的輸入增加一個控制信號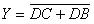 ,那么當DCBA=1010~1111時,不論a~g是1還是0,
,那么當DCBA=1010~1111時,不論a~g是1還是0,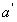 ~
~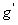 肯定等于0,所以
肯定等于0,所以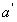 ~
~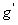 仍然符合表1.2.1的要求。
仍然符合表1.2.1的要求。
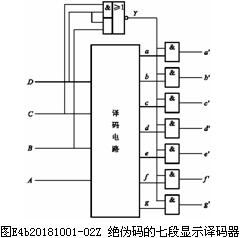
這就是說,當DCBA取值為1010~1111時,a~g每個函數輸出的取值是1或0都可以,不影響最后的輸出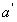 ~
~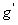 。因此,在DCBA取值為1010~1111時,其值為1的六個最小項
。因此,在DCBA取值為1010~1111時,其值為1的六個最小項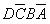 、
、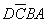 、
、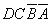 、
、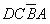 、
、 和為
和為 數a~g的任意項。在化簡a~g的邏輯函數式時,既可以在式中寫入這些任意項,也可以不寫進這些任意項,所以任意項也是邏輯函數式中的無關項。這樣我們就可以把表1.2.1改寫為表1.2.2的形式了。表中的×仍然表示無關項。
數a~g的任意項。在化簡a~g的邏輯函數式時,既可以在式中寫入這些任意項,也可以不寫進這些任意項,所以任意項也是邏輯函數式中的無關項。這樣我們就可以把表1.2.1改寫為表1.2.2的形式了。表中的×仍然表示無關項。
雖然任意項和約束項都是邏輯函數式中的無關項,但二者是有區別的。因為約束項的取值永遠是0,所以在邏輯函數式中無論寫入約束項還是去掉約束項,都不會改變函數的輸出值。而任意項則不同,當我們在邏輯函數式中寫入某個任意項之后,則輸入變量的取值使這個任意項的值為1時,函數的輸出值也為1;如果從邏輯函數式中將這個任意項拿掉,則輸入變量取值使這個任意項的值為1時,函數的輸出值等于0。
【題目5】:如何判斷一個邏輯函數已化到了最簡?化簡邏輯函數有什么實際意義?
【相關知識】:邏輯函數的與或表達式和邏輯函數的代數法化簡等。
【解題方法】:為了便于實現邏輯電路,邏輯函數常用“與或”表達式表示。因此,是否化到最簡主要看與項數目和每個與項所包含的變量數是否最少。
【解答過程】:一個與或表達式是否已達到最簡,主要看兩個方面:一是表達式中“與”項的數目是否最少了,即表達式中的與項是否不能再合并了;第二是在與項相同的條件下,檢查每個與項所包含的變量數是否達到了最少。因為減少與項可以節省與門個數,減少與項中的變量數可以減少門的輸入端個數。
【題目6】:邏輯函數的不同表示方法之間是如何進行轉換的?
【相關知識】:邏輯函數真值表、邏輯函數的與或表達式、卡諾圖、最小項、標準與或表達式。
【解題方法】:通過1.由真值表求邏輯函數式;2.由邏輯函數式求真值表;3.卡諾圖與邏輯函數表達式之間的轉換,一、一加以說明。
【解答過程】:同一個邏輯問題,可以采用多種方法表示。而這些描述同一個問題的邏輯表示之間都能實現方便的轉換。
1.由真值表求邏輯函數式和邏輯電路
把真值表中使邏輯函數值為1的輸入變量組合寫成對應的與項。若對應的變量取值為1,則寫成原變量;若對應的變量取值為0,則寫成反變量。然后將這些與項全部“或”起來,就得到了邏輯函數式。
對應于邏輯函數式的反變量,采用非門邏輯符號;與項用與門邏輯符號,多個與項相“或”用或門邏輯符號;將它們按邏輯運算關系連接起來,就能得到實現邏輯要求的邏輯電路。
2. 由邏輯函數式求真值表
只要把邏輯函數式中所有輸入變量按“0”、“1”取值,代入所有組合中(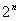 —n是函數的變量數)進行運算,求出相應的邏輯函數值(結果)填入真值表中的相應行即可。
—n是函數的變量數)進行運算,求出相應的邏輯函數值(結果)填入真值表中的相應行即可。
3. 卡諾圖與邏輯函數表達式之間的轉換
先將邏輯函數化為最小項之和的形式(即標準與或表達式),接著畫出與函數變量數相對應的卡諾圖,在卡諾圖中,凡是與表達式對應的最小項的小方格內填入“1”,其他小方格內填入“0”。這樣便得到了邏輯函數式的卡諾圖。
【題目7】:正負邏輯門電路符號間有什么對應的關系如何?
【相關知識】:正負邏輯的定義。
【解題方法】:通過真值表表示正負邏輯,能比較清楚地理解正負邏輯之間的關系。
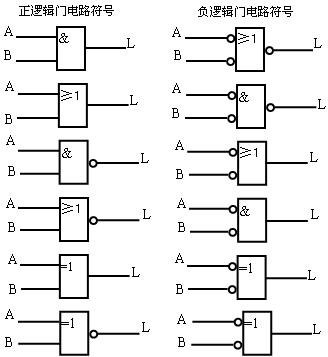
【解答過程】:我們知導,高電平用“1”表示,低電平用“0”表示,是正邏輯的定義;如果高電平定義為“0”,低電平定義為“1”,這是負邏輯的定義。因此以2個變量為例,當結果為“1”時,正邏輯表示的“與”邏輯真值表對應于負邏輯表示的“或”邏輯真值表。圖示是幾種常用正負邏輯之間的對應關系。

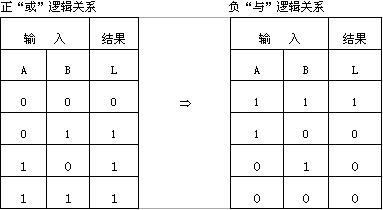
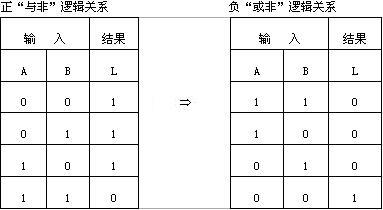
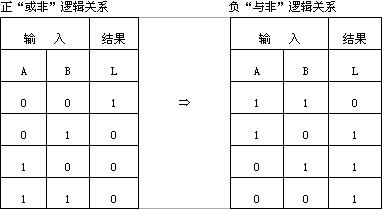
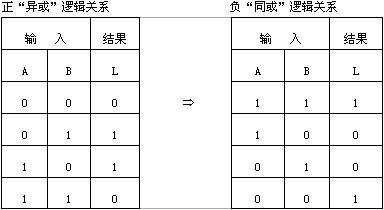
邏輯符號間的對應關系為:
【題目8】:怎樣讓一個邏輯函數用最小項之和表示或者用最大項之積表示?
【相關知識】:邏輯函數的化簡,反函數的概念,最小項,最大項。
【解題方法】:同一個邏輯關系可以用兩種標準的函數表達式表示,實際上是一種互補的表示方法。
【解答過程】:大家知道,包含n個變量的邏輯函數,可以用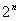 個標準的與項之和形式表示出來。那么什么是標準“與項”呢?
個標準的與項之和形式表示出來。那么什么是標準“與項”呢?
假如一個函數有三個變量A、B、C,則它最多有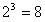 個標準的與項(最小項),
個標準的與項(最小項),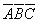 、
、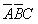 、
、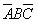 、
、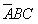 、
、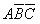 、
、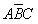 、
、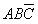 、
、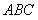 。
。
一個函數表達式假如是由各最小項之和表示的,則該表達式就稱為最小項之和表達式。如: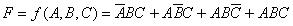
顯然,同一個邏輯函數,也可用標準的或項之積表示。這標準的或項就是最大項。
如上述的邏輯函數有3個變量,所以有8個最小項,但函數中只出現4個,這4個最小項取值為1,而另外4個最小項取值為0。因此,我們也可以用反函數的形式寫出該表達式,即: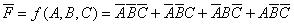
將兩邊同時求反,便可變為原函數:
【題目9】:畫卡諾圖時,具有二個變量以上的邏輯函數的邏輯相鄰性如何確定?有何規律?
【相關知識】:最小項,卡諾圖,邏輯相鄰性,循環碼(格雷碼)。
【解題方法】:根據循環碼的任何相鄰二組代碼之間只有一個變量不同,這正好與卡諾圖小方格的要求一致。
【解答過程】:大家知道,循環碼(即格雷碼)具有這樣的特征:任何相鄰二組代碼之間只存在一個不同變量,這一點正好與邏輯相鄰性定義一致,(只有一個變量不同的二個與項,邏輯上稱其為相鄰)。
因此,在畫多變量卡諾圖時,按循環碼規律就能得到正確的卡諾圖。
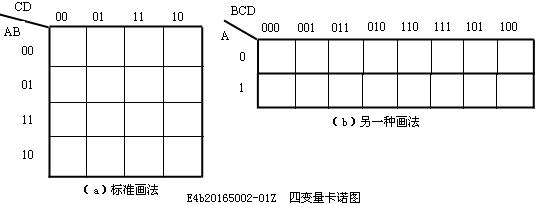
如四變量(A、B、C、D)卡諾圖,分別有四行、四列,它們分別按二變量的循環碼排列:列AB按00、01、11、10排序;行 CD按00、01、11、10循環碼排列。四變量卡諾圖如圖所示,圖(a)是標準畫法,圖(b)是另一種畫法,但不管是二變量還是三變量,都是按照格萊碼規律排列的。
【題目10】:具有無關項的邏輯函數如何化簡?
【相關知識】:卡諾圖,無關項,最小項,具有約束的邏輯函數。
【解題方法】:正確認識邏輯變量組合與邏輯結果之間關系,無關項在一個邏輯函數中的表示方法,正確認識無關項在一個邏輯函數的化簡中,可以當作“1”和當作“0”處理。
【解答過程】:對于邏輯函數中的無關項,可以用幾種方法給出。例如,某邏輯電路的輸入信號DCBA是8421 BCD碼,由8421 BCD碼概念可知:如下的變量組合(即最小項)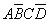 ,
,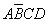 ,
,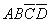 ,
, ,
,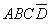 ,
,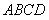 是不會出現的,即不影響8421BCD編碼結果,所以這些項就是無關項。在邏輯函數化簡時,正因為這些項無關,因此這些項的取值可以認為是“0”,也可以認為是“1”,這由你的簡化程度來決定。
是不會出現的,即不影響8421BCD編碼結果,所以這些項就是無關項。在邏輯函數化簡時,正因為這些項無關,因此這些項的取值可以認為是“0”,也可以認為是“1”,這由你的簡化程度來決定。
若將具有無關項的邏輯函數表示在卡諾圖中,圖中填1和0的小方格分別對應于函數式中的最小項和式中不出現的最小項。卡諾圖中無關項對應處填“×”以示區別。“×”的小方格可以和“1”格一起包圍,此時,在包圍圈中的無關項當1對待;“×”的小方格可以不被包圍,這時的“×”小方格就當作“0”處理了。
在用表達式化簡時,可以將無關項當作“1”寫入表達式中,以便和其它項相結合,使表達式化得更加簡單些。如果該無關項對式子的簡化無幫助,則就當作“0”處理。
以下是用卡諾圖化簡和用表達式化簡的兩種例子。如要求對下列邏輯函數化簡:
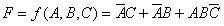 (無關項為:
(無關項為: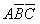 ,
,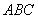 )
)
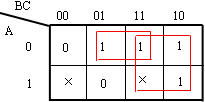
結合“1”方格畫包圍圈得: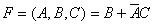 ,這里是把“111”格當作“1”處理,而把“100”格當作“0”了。
,這里是把“111”格當作“1”處理,而把“100”格當作“0”了。
用表達式化簡過程如下:
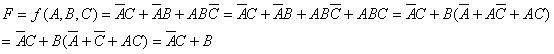
顯然,表達式中將添加的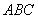 當作“1”,而將(f29)無關項作“0”處理,兩者化簡的結果完全相同。
當作“1”,而將(f29)無關項作“0”處理,兩者化簡的結果完全相同。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底