一、最小項(xiàng)
1．最小項(xiàng)的特點(diǎn)（以三變量A，B，C為例）每項(xiàng)都只有三個因子（A，B，C）；每個變量都是它的一個因子；每一變量或以原變量(A，B，C)形式出現(xiàn)，或以非變量(A非，B非，C非)形式出現(xiàn)；每個乘積項(xiàng)的組合僅出現(xiàn)一次，且取值為
1；最小項(xiàng)可以編碼。
2．最小項(xiàng)表達(dá)式及書寫形式：最小項(xiàng)表達(dá)式是由若干個最小項(xiàng)相加的與—或表達(dá)式。任何一個邏輯表達(dá)式都可以化成最小項(xiàng)表達(dá)式。
2.一個邏輯函數(shù)，如果有n個變量，則有2ⁿ個最小項(xiàng)。
最小項(xiàng)的基本性質(zhì)：

• a．只有一組取值使之為“1”
• b．任二最小項(xiàng)乘積與“0”
• c．所的最小項(xiàng)之和為“1”

例：3變量A，B，C，有2³＝8個最小項(xiàng)，其形式為：


二、卡諾圖（Karnaugh Map）

1．卡諾圖畫法：

三變量卡諾圖: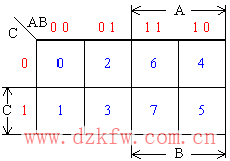

說明:三變量卡諾圖由8個最小項(xiàng)m₀—m₇組成，每個最小項(xiàng)占一個方格；
AB組合中左數(shù)位代表A變量，右數(shù)位代表B變量。沿橫向從一個方格進(jìn)行到下一個方格時，兩個數(shù)位只變化一個； 原變量與非變量各占4格。
四變量卡諾圖: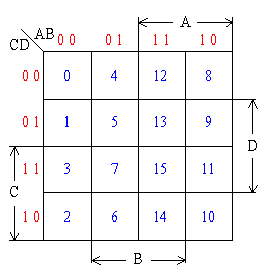

說明:
四變量卡諾圖由16個最小項(xiàng)m₀—m₁₅組成，每個最小項(xiàng)占一個方格；縱向方向因有兩個變量CD，增加了8個方格，CD變化規(guī)律同AB；原變量與非變量各占8格。（http://www.shkcfs.com/版權(quán)所有 )
2．相鄰的概念

二小格相鄰組合:
例如:卡諾圖中，有F（A，B，C，D）=∑m(2，3，8，10，12)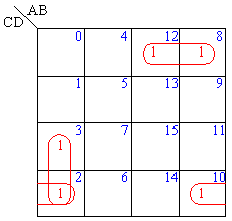

（m₈、m₁₂）、（m₂、m₃）幾何相鄰，（m₂、m₁₀）邏輯相鄰
四小格相鄰組合：四小格相鄰時，4個最小項(xiàng)可合并成1項(xià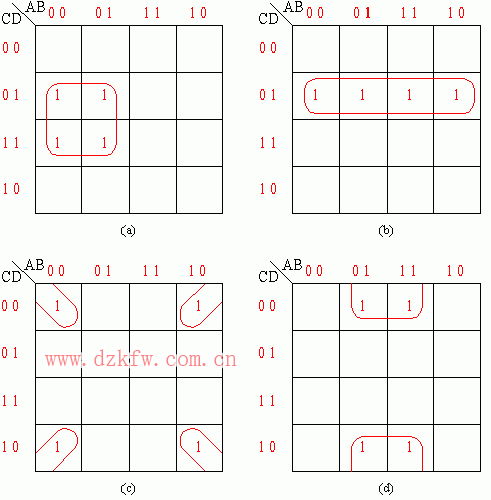ng)，且可消去兩個變量。

八方格相鄰組合：
八方格相鄰時，8個最小項(xiàng)可合并成1項(xià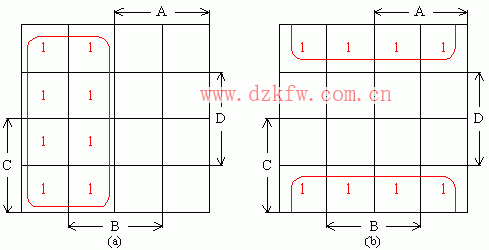ng)，且可消去三個變量。

三、用卡諾圖簡化邏輯函數(shù)

1． 用卡諾圖化簡邏輯函數(shù)基本步驟：

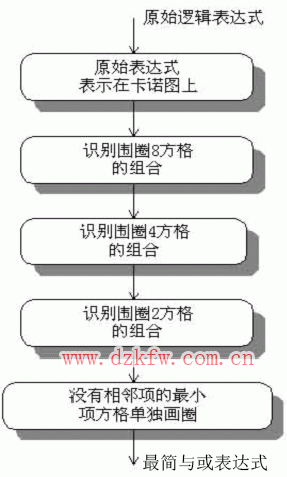
2．幾個注意點(diǎn)：

1. 必須使每個方格(最小項(xiàng))至少被包含一次；
2. 使每個組合包含盡可能多的方格；
3. 所有的方格包含在盡可能少的不同組合中。
4. 未用最小項(xiàng)表示的邏輯函數(shù)的簡化：邏輯函數(shù)未用(最小項(xiàng))表示照樣可以化簡。如果F采用與—或表達(dá)式，在填入卡諾圖過程中先把函數(shù)展開成標(biāo)準(zhǔn)與--或式，再填入卡諾圖中進(jìn)行化簡。

3． 具有約束項(xiàng)的邏輯函數(shù)的化簡

任意項(xiàng)又叫無關(guān)項(xiàng)，是一種最小項(xiàng)，其值可以取0或1。利用任意項(xiàng)這一特點(diǎn)，可以使函數(shù)簡化。 任意項(xiàng)用“×”（或“d”）表示，利用無關(guān)項(xiàng)化簡原則：① 無關(guān)項(xiàng)即可看作“1”也可看作“0”。②卡諾圖中，圈組內(nèi)的“×”視為“1”，圈組外的視為“0”。