一、卡諾圖概念

　　卡諾圖是邏輯函數(shù)的一種圖形表示。一個(gè)邏輯函數(shù)的卡諾圖就是將此函數(shù)的最小項(xiàng)表達(dá)式中的各最小項(xiàng)相應(yīng)地填入一個(gè)方格圖內(nèi)，此方格圖稱(chēng)為卡諾圖�？ㄖZ圖的構(gòu)造特點(diǎn)使卡諾圖具有一個(gè)重要性質(zhì)：可以從圖形上直觀地找出相鄰最小項(xiàng)。兩個(gè)相鄰最小項(xiàng)可以合并為一個(gè)與項(xiàng)并消去一個(gè)變量。

　　二、卡諾圖結(jié)構(gòu)特點(diǎn)

　　卡諾圖中最小項(xiàng)的排列方案不是唯一的，變量的坐標(biāo)值0表示相應(yīng)變量的反變量，1表示相應(yīng)變量的原變量，變量的取值變化規(guī)律按“循環(huán)碼”變化［1］。各小方格依變量順序取坐標(biāo)值，所得二進(jìn)制數(shù)對(duì)應(yīng)的十進(jìn)制數(shù)即相應(yīng)最小項(xiàng)的下標(biāo)i。

　　在五變量卡諾圖中，為了方便省略了符號(hào)“m”，直接標(biāo)出m的下標(biāo)i。

　　歸納起來(lái)，卡諾圖在構(gòu)造上具有以下兩個(gè)特點(diǎn)：

　　☆n個(gè)變量的卡諾圖由2^n個(gè)小方格組成，每個(gè)小方格代表一個(gè)最小項(xiàng)；

　　☆卡諾圖上處在相鄰、相對(duì)、相重位置的小方格所代表的最小項(xiàng)為相鄰最小項(xiàng)。

　　可以從圖形上直觀地找出相鄰最小項(xiàng)。兩個(gè)相鄰最小項(xiàng)可以合并為一個(gè)與項(xiàng)并消去一個(gè)變量。

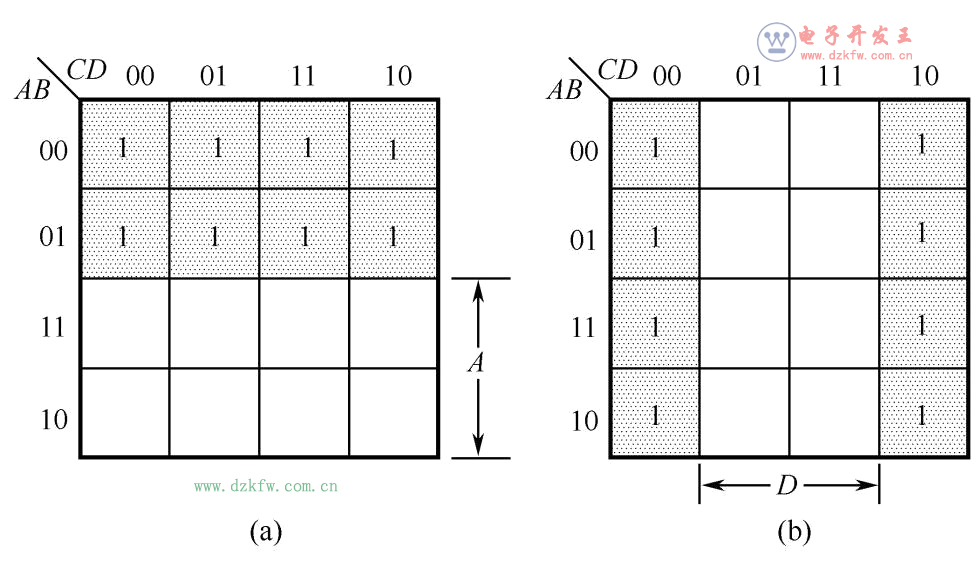
　　三、卡諾圖的性質(zhì)

　　卡諾圖的構(gòu)造特點(diǎn)使卡諾圖具有一個(gè)重要性質(zhì)：可以從圖形上直觀地找出相鄰最小項(xiàng)合并。合并的理論依據(jù)是并項(xiàng)定理AB+AB=A。例如，

　　根據(jù)定理AB+AB=A和相鄰最小項(xiàng)的定義，兩個(gè)相鄰最小項(xiàng)可以合并為一個(gè)與項(xiàng)并消去一個(gè)變量。例如，4變量最小項(xiàng)ABCD和ABCD相鄰，可以合并為ABD；ABCD和ABCD相鄰，可以合并為ABD；而與項(xiàng)ABD和ABD又為相鄰與項(xiàng)，故按同樣道理可進(jìn)一步將兩個(gè)相鄰與項(xiàng)合并為BD。

　　用卡諾圖化簡(jiǎn)邏輯函數(shù)的基本原理就是把上述邏輯依據(jù)和圖形特征結(jié)合起來(lái)，通過(guò)把卡諾圖上表征相鄰最小項(xiàng)的相鄰小方格“圈”在一起進(jìn)行合并，達(dá)到用一個(gè)簡(jiǎn)單“與”項(xiàng)代替若干最小項(xiàng)的目的。

　　通常把用來(lái)包圍那些能由一個(gè)簡(jiǎn)單“與”項(xiàng)代替的若干最小項(xiàng)的“圈”稱(chēng)為卡諾圈。

　　邏輯函數(shù)在卡諾圖上的表示

　　1．給定邏輯函數(shù)為標(biāo)準(zhǔn)“與-或”表達(dá)式

　　當(dāng)邏輯函數(shù)為標(biāo)準(zhǔn)“與-或”表達(dá)式時(shí)，只需在卡諾圖上找出和表達(dá)式中最小項(xiàng)對(duì)應(yīng)的小方格填上1，其余小方格填上0，即可得到該函數(shù)的卡諾圖。

　　例如，3變量函數(shù)F（A，B，C）=∑m（1，2，3，7）的卡諾圖如圖2．6所示。

　　圖2．6函數(shù)F（A，B，C）=∑m（1，2，3，7）的卡諾圖

　　2．邏輯函數(shù)為一般“與-或”表達(dá)式

　　當(dāng)邏輯函數(shù)為一般“與-或”表達(dá)式時(shí)，可根據(jù)“與”的公共性和“或”的疊加性作出相應(yīng)卡諾圖。

　　例如，4變量函數(shù)F（A，B，C，D）=AB+CD+A·BC的卡諾圖如圖2．7所示。

　　圖2．7函數(shù)F（A，B，C，D）=AB+CD+A·BC的卡諾圖

　　填寫(xiě)該函數(shù)卡諾圖時(shí)，只需在4變量卡諾圖上依次找出和“與項(xiàng)”AB、CD、A·BC對(duì)應(yīng)的小方格填上1，便可得到該函數(shù)的卡諾圖。

　　當(dāng)邏輯函數(shù)表達(dá)式為其他形式時(shí)，可將其變換成上述形式后再作卡諾圖。

　　為了敘述的方便，通常將卡諾圖上填1的小方格稱(chēng)為1方格，填0的小方格稱(chēng)為0方格。0方格有時(shí)用空格表示。

　　四、卡諾圖化簡(jiǎn)邏輯函數(shù)

　　1．幾個(gè)定義

　　蘊(yùn)涵項(xiàng)：在函數(shù)的“與-或”表達(dá)式中，每個(gè)“與”項(xiàng)被稱(chēng)為該函數(shù)的蘊(yùn)涵項(xiàng)（Implicant）。

　　顯然，在函數(shù)卡諾圖中，任何一個(gè)1方格所對(duì)應(yīng)的最小項(xiàng)或者卡諾圈中的2m個(gè)1方格所對(duì)應(yīng)的“與”項(xiàng)都是函數(shù)的蘊(yùn)涵項(xiàng)。

　　質(zhì)蘊(yùn)涵項(xiàng)：若函數(shù)的一個(gè)蘊(yùn)涵項(xiàng)不是該函數(shù)中其他蘊(yùn)涵項(xiàng)的子集，則此蘊(yùn)涵項(xiàng)稱(chēng)為質(zhì)蘊(yùn)涵項(xiàng)（PrimeImplicant），簡(jiǎn)稱(chēng)為質(zhì)項(xiàng)。

　　顯然，在函數(shù)卡諾圖中，按照最小項(xiàng)合并規(guī)律，如果某個(gè)卡諾圈不可能被其他更大的卡諾圈包含，那么，該卡諾圈所對(duì)應(yīng)的“與”項(xiàng)為質(zhì)蘊(yùn)涵項(xiàng)。

　　必要質(zhì)蘊(yùn)涵項(xiàng)：若函數(shù)的一個(gè)質(zhì)蘊(yùn)涵項(xiàng)包含有不被函數(shù)的其他任何質(zhì)蘊(yùn)涵項(xiàng)所包含的最小項(xiàng)，則此質(zhì)蘊(yùn)涵項(xiàng)被稱(chēng)為必要質(zhì)蘊(yùn)涵項(xiàng)（EssenTIalPrimeImplicant），簡(jiǎn)稱(chēng)為必要質(zhì)項(xiàng)。

　　在函數(shù)卡諾圖中，若某個(gè)卡諾圈包含了不可能被任何其他卡諾圈包含的1方格，那么，該卡諾圈所對(duì)應(yīng)的“與”項(xiàng)為必要質(zhì)蘊(yùn)涵項(xiàng)。

　　2．求函數(shù)最簡(jiǎn)“與-或”表達(dá)式

　�。�1）一般步驟：

　　第一步：作出函數(shù)的卡諾圖。

　　第二步：在卡諾圖上圈出函數(shù)的全部質(zhì)蘊(yùn)涵項(xiàng)。按照卡諾圖上最小項(xiàng)的合并規(guī)律，對(duì)函數(shù)F卡諾圖中的1方格畫(huà)卡諾圈。為了圈出全部質(zhì)蘊(yùn)涵項(xiàng)，畫(huà)卡諾圈時(shí)在滿(mǎn)足合并規(guī)律的前題下應(yīng)盡可能大，若卡諾圈不可能被更大的卡諾圈包圍，則對(duì)應(yīng)的“與”項(xiàng)為質(zhì)蘊(yùn)涵項(xiàng)。

　　第三步：從全部質(zhì)蘊(yùn)涵項(xiàng)中找出所有必要質(zhì)蘊(yùn)涵項(xiàng)。在卡諾圖上只被一個(gè)卡諾圈包圍的最小項(xiàng)被稱(chēng)為必要最小項(xiàng)，包含必要最小項(xiàng)的質(zhì)蘊(yùn)涵項(xiàng)即必要質(zhì)蘊(yùn)涵項(xiàng)。為了保證所得結(jié)果無(wú)一遺漏地覆蓋函數(shù)的所有最小項(xiàng)，函數(shù)表達(dá)式中必須包含所有必要質(zhì)蘊(yùn)涵項(xiàng)。

　　第四步：求出函數(shù)的最簡(jiǎn)質(zhì)蘊(yùn)涵項(xiàng)集。若函數(shù)的所有必要質(zhì)蘊(yùn)涵項(xiàng)尚不能覆蓋卡諾圖上的所有1方格，則從剩余質(zhì)蘊(yùn)涵項(xiàng)中找出最簡(jiǎn)的所需質(zhì)蘊(yùn)涵項(xiàng)，使它和必要質(zhì)蘊(yùn)涵項(xiàng)一起構(gòu)成函數(shù)的最小覆蓋。

　　（2）舉例

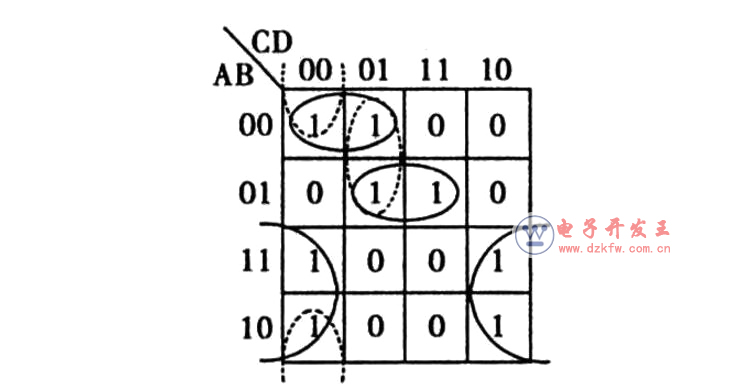
　　例1用卡諾圖化簡(jiǎn)邏輯函數(shù)F（A，B，C，D）=∑m（0，3，5，6，7，10，11，13，15）。

　　解根據(jù)卡諾圖化簡(jiǎn)的步驟，該題化簡(jiǎn)過(guò)程如下：

　　該題中，5個(gè)必要質(zhì)蘊(yùn)涵項(xiàng)已將函數(shù)的全部最小項(xiàng)覆蓋，故將各卡諾圈對(duì)應(yīng)的與項(xiàng)相或即可得到函數(shù)F的最簡(jiǎn)“與-或”表達(dá)式為

　　F（A，B，C，D）=A·B·C·D+ABC+ABC+BD+CD

　　例2用卡諾圖化簡(jiǎn)邏輯函數(shù)F（A，B，C，D）=∑m（2，3，6，7，8，10，12）。

　　解根據(jù)卡諾圖化簡(jiǎn)的步驟，該題化簡(jiǎn)過(guò)程如下：

　　由圖可知，該函數(shù)包含兩個(gè)必要質(zhì)蘊(yùn)涵項(xiàng)，即AC和AC·D。在選取必要質(zhì)蘊(yùn)涵項(xiàng)之后，尚有最小項(xiàng)m10未被覆蓋。為了覆蓋最小項(xiàng)m10，可選質(zhì)蘊(yùn)涵項(xiàng)BCD或者AB·D，由于這兩個(gè)質(zhì)蘊(yùn)涵項(xiàng)均由3個(gè)變量組成，故可任選其中之一作為所需質(zhì)蘊(yùn)涵項(xiàng)，即F的最簡(jiǎn)質(zhì)蘊(yùn)涵項(xiàng)集可為

　　{AC，AC·D，BCD}或者{AC，AC·D，AB·D}

　　因而，可求得函數(shù)F的最簡(jiǎn)“與-或”表達(dá)式為

　　F（A，B，C，D）=AC+AC·D+BCD或者F（A，B，C，D）=AC+AC·D+AB·D

　　這里，函數(shù)F的最簡(jiǎn)“與-或”式有兩個(gè)，其復(fù)雜程度相同。由此可見(jiàn)，一個(gè)函數(shù)的最簡(jiǎn)“與-或”表達(dá)式不一定是唯一的！

　　歸納起來(lái)，卡諾圖化簡(jiǎn)的原則是：

　　☆在覆蓋函數(shù)中的所有最小項(xiàng)的前提下，卡諾圈的個(gè)數(shù)達(dá)到最少。

　　☆在滿(mǎn)足合并規(guī)律的前題下卡諾圈應(yīng)盡可能大。

　　☆根據(jù)合并的需要，每個(gè)最小項(xiàng)可以被多個(gè)卡諾圈包圍。

　　3.求函數(shù)的最簡(jiǎn)“或-與”表達(dá)式

　　當(dāng)需要求一個(gè)函數(shù)的最簡(jiǎn)“或-與”表達(dá)式時(shí)，可采用“兩次取反法”。

　　具體如下：

　　☆先求出函數(shù)F的反函數(shù)F的最簡(jiǎn)“與-或”表達(dá)（合并卡諾圖上的0方格）；

　　☆然后對(duì)F的最簡(jiǎn)“與-或”表達(dá)式取反，從而得到函數(shù)F的最簡(jiǎn)“或-與”表達(dá)式。

　　例如，用卡諾圖求邏輯函數(shù)F（A，B，C，D）=∑m（3，4，6，7，11，12，13，14，15）的最簡(jiǎn)“或-與”表達(dá)式。

　　解首先畫(huà)出函數(shù)F的卡諾圖如圖2．13所示。

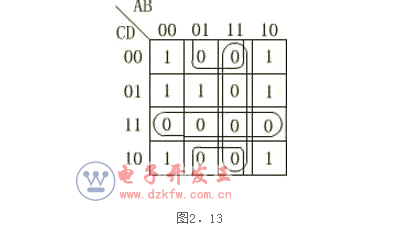
　　圖中，F(xiàn)的0方格即反函數(shù)F的1方格，它們代表F的各個(gè)最小項(xiàng)，將全部0方格合并就可得到反函數(shù)F的最簡(jiǎn)“與-或”表達(dá)式

　　F（A，B，C，D）=AB+CD+BD

　　再對(duì)上述函數(shù)式兩邊取反，即可求得函數(shù)的最簡(jiǎn)“或-與”表達(dá)式

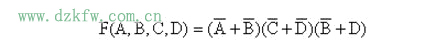
　　卡諾圖化簡(jiǎn)邏輯函數(shù)具有方便、直觀、容易掌握等優(yōu)點(diǎn)。但依然帶有試湊性。尤其當(dāng)變量個(gè)數(shù)大于6時(shí)，畫(huà)圖以及對(duì)圖形的識(shí)別都變得相當(dāng)復(fù)雜。